Continuidade de uma função num ponto

Seja uma função real de variável real cujo domínio contenha pelo menos um intervalo aberto , em que a < b coma, b ∈ e seja c ∈ .

Então diz-se uma função contínua em c se e só se:

• 

Em particular, seja uma função real de variável real cujo domínio contenha pelo menos um intervalo aberto , em que a < b com a, b ∈ e seja c ∈ .

Então diz-se uma função contínua à esquerda de c se e só se:

• Da mesma forma, seja uma função real de variável real cujo domínio contenha pelo menos um intervalo aberto , em que a < b com a, b ∈ e seja c ∈ .

Então diz-se uma função contínua à direita de c se e só se:

• Mas se uma função real de variável real for contínua num ponto c, é necessariamente contínua à esquerda de c e é contínua à direita de c.

Propriedades de funções contínuas num ponto c:

Se e forem duas funções reais de variável real e contínuas em c, sendo que , são também contínuas em as seguintes composições de e de :

- A função soma +

- A função diferença -

- A função produto x

- A função quociente desde que g(c) ≠ 0

- A função potência de expoente n, com n ∈

- A função raiz de índice n, com n ∈ e 0 no caso de n ser par

- A própria função composta 0 é contínua em c, com c ∈ , se e só se for contínua em c, e for contínua em g(c).

Resumindo:

Uma função é contínua se:

• a ∈ Df
• existe
• =

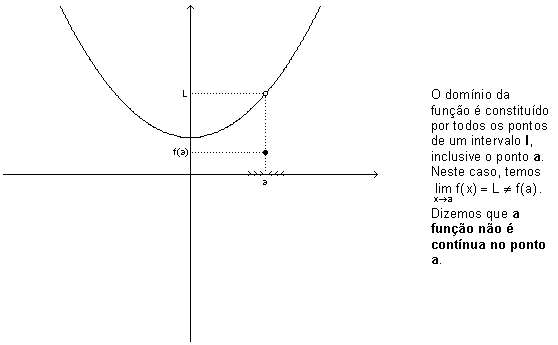
Exemplo de uma função não contínua: